Problem Statement:
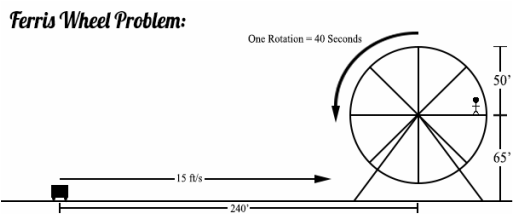
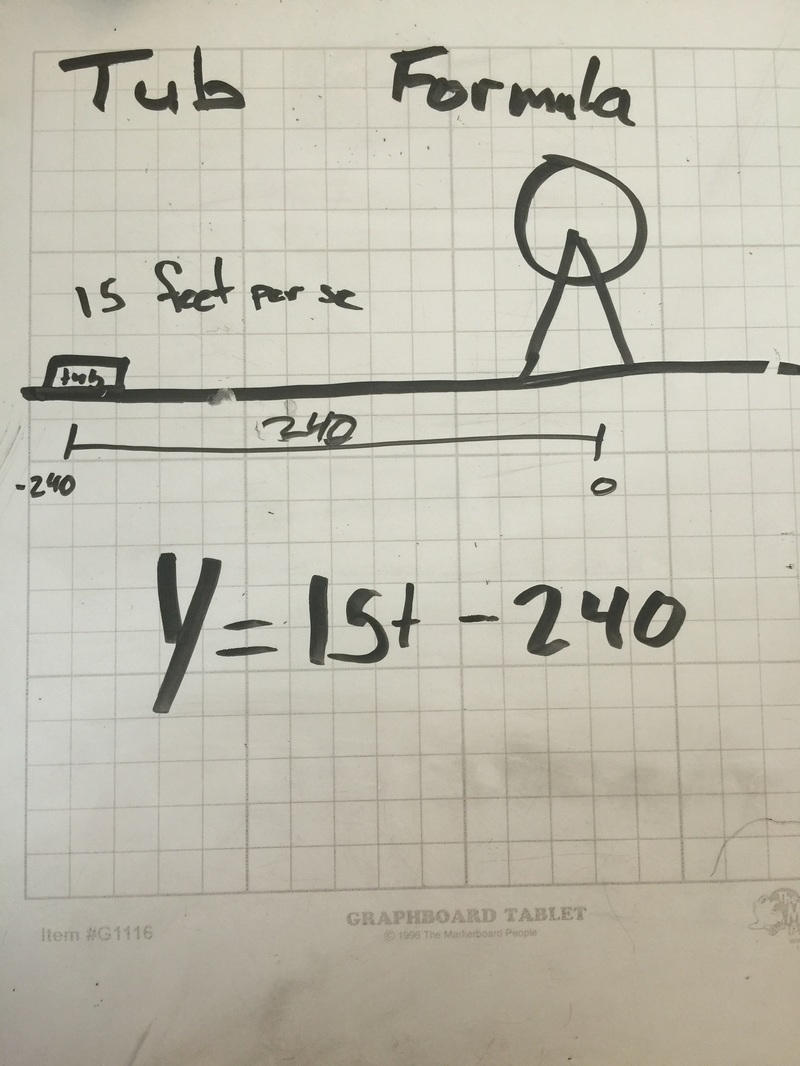
The ferris wheel we were working on center is 65 feet from the ground and had a radius of 50 feet. Located on the circumference of the ferris wheel is diver and his assistant who spin counterclockwise starting at 3:00 o’clock. A tub of water is constantly moving on a track that is parallel to the ferris wheel’s plane and moves on the ground. The tub starts 240 feet to the left of the center of the ferris wheel and the water in the tub is 8 feet from the ground. The divers assistant must determine the exact moment to release the diver from a platform suspended from a moving ferris wheel so that he lands in the tub of water.
Formulas:
The ferris wheel we were working on center is 65 feet from the ground and had a radius of 50 feet. Located on the circumference of the ferris wheel is diver and his assistant who spin counterclockwise starting at 3:00 o’clock. A tub of water is constantly moving on a track that is parallel to the ferris wheel’s plane and moves on the ground. The tub starts 240 feet to the left of the center of the ferris wheel and the water in the tub is 8 feet from the ground. The divers assistant must determine the exact moment to release the diver from a platform suspended from a moving ferris wheel so that he lands in the tub of water.
Formulas:
- Height at any given time of diver= 50sin(9t)+65
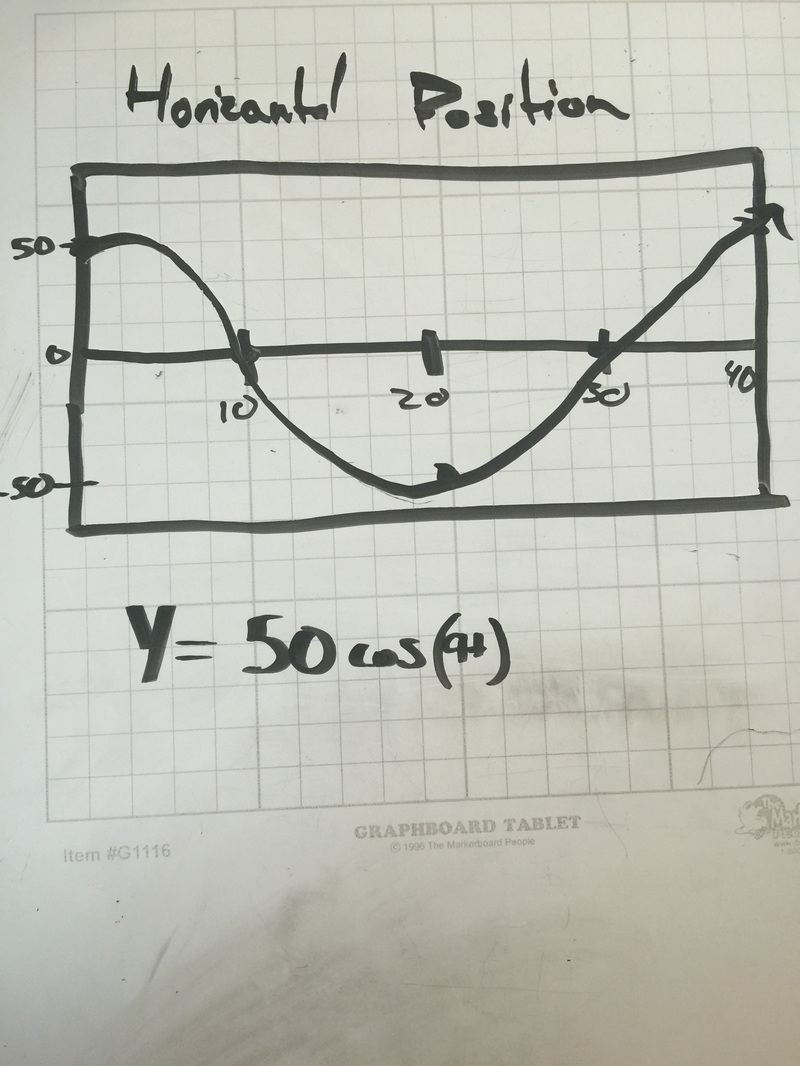
- Horizontal Position of diver= 50cos(9t)
- Speed and position of tub y=15t-240
- Drop time sqr(h/16)
Process:
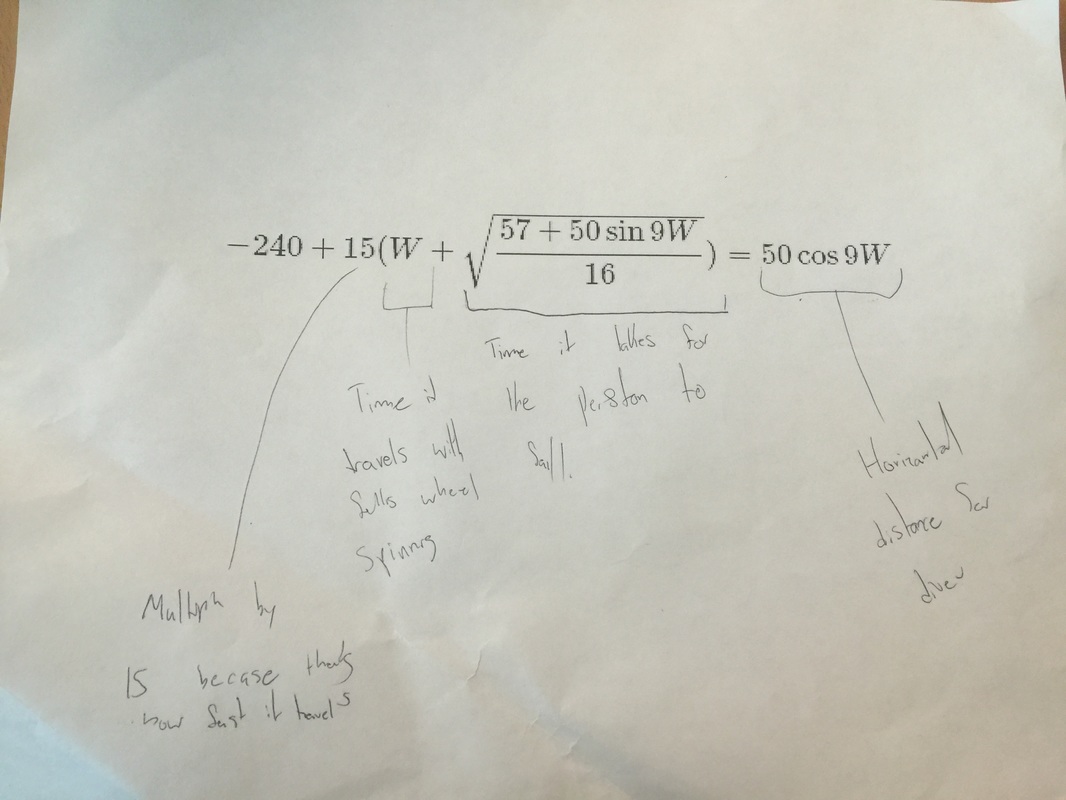
Here is where I will derive the formula I got for the Ferris Wheel Problem.
((((50sin(9t) + 65) / (16))^(1/2)) * 15) + 15t = 50co(9t) + 240
RED = The first Part of the equation corresponds to the vertical position of the diver after t amount of seconds. You input a time in seconds and it will tell you at what high the diver with be.
PINK = Is the formula to calculate the fall time of an object from the high imputed
ORANGE = Multiplying the seconds we get with the speed of the tub gives us the distance it covers in the time the object is falling.
BLUE = By adding it to 15t which is how much distance the tub covered while the ferris wheel was moving we get the total distance the tub will cover.
PURPLE = When you plug in a time in seconds into the purple it gives you the horizontal position of where the diver will be after those many seconds.
GREEN = We add 240 because that the total distance the tub has to cover and if we compare the divers distance with the tub we can get an exact number for when the diver should dive.
Here is where I will derive the formula I got for the Ferris Wheel Problem.
((((50sin(9t) + 65) / (16))^(1/2)) * 15) + 15t = 50co(9t) + 240
RED = The first Part of the equation corresponds to the vertical position of the diver after t amount of seconds. You input a time in seconds and it will tell you at what high the diver with be.
PINK = Is the formula to calculate the fall time of an object from the high imputed
ORANGE = Multiplying the seconds we get with the speed of the tub gives us the distance it covers in the time the object is falling.
BLUE = By adding it to 15t which is how much distance the tub covered while the ferris wheel was moving we get the total distance the tub will cover.
PURPLE = When you plug in a time in seconds into the purple it gives you the horizontal position of where the diver will be after those many seconds.
GREEN = We add 240 because that the total distance the tub has to cover and if we compare the divers distance with the tub we can get an exact number for when the diver should dive.
Solution:
When we solved the equation we got 12.2828 secs when they meet exactly in the middle. At around 13 secs the diver and tub would be perfectly one on top of the other but because of drop time we had to have the diver drop a slight bit earlier.
Journal Prompt:
How can we make the problem harder?
I had an idea to make the problem happen on the moon which would make us have a different formula for the fall time. Because the gravitational pull is not as high as on earth it would be a harder problem.
When we solved the equation we got 12.2828 secs when they meet exactly in the middle. At around 13 secs the diver and tub would be perfectly one on top of the other but because of drop time we had to have the diver drop a slight bit earlier.
Journal Prompt:
How can we make the problem harder?
I had an idea to make the problem happen on the moon which would make us have a different formula for the fall time. Because the gravitational pull is not as high as on earth it would be a harder problem.
Problem Assessment:
Overall I really enjoyed this problem a lot and I liked how many steps it took to have to get to the solution. When presented it seems pretty easy but because the falling time is too essential we had to do a lot of steps to make sure that our process was correct.
Self Evaluation:
I worked hard on this problem because it intrigued me and I wanted to get to the answer. When I started on the problem I started a little slow but at the end I really wanted to solve it and have a step by step explanation on how to solve the ferris wheel problem.
Overall I really enjoyed this problem a lot and I liked how many steps it took to have to get to the solution. When presented it seems pretty easy but because the falling time is too essential we had to do a lot of steps to make sure that our process was correct.
Self Evaluation:
I worked hard on this problem because it intrigued me and I wanted to get to the answer. When I started on the problem I started a little slow but at the end I really wanted to solve it and have a step by step explanation on how to solve the ferris wheel problem.


 RSS Feed
RSS Feed
